EM Feld Simulation
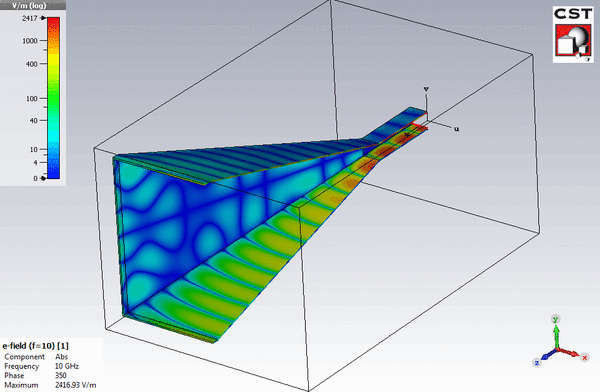
EM field simulations are becoming increasingly indispensable in the research and development of complex electronic devices. They help to understand complicated interactions between electromagnetic fields and the components of the application in order to optimize them. Meanwhile field simulations are used in many fields, such as antenna and PCB development, EMC and EMCU or for the calculation of magnetic flux densities in electric motors.
With professional EM field simulators, it is possible not only to calculate electromagnetic fields and the variables derived from them (e.g. specific absorption rate SAR, Total Radiated Power TRP, etc.) but also to determine the distribution of temperature and mechanical deformation. In addition to the field simulator, a circuit simulator is often integrated in these software packages, so that a complete circuit, the passive structure with the concentrated components, can be simulated and optimized.
The enormous progress in computer technology and the availability of inexpensive computer resources now also allow the parameterization and optimization of very large models in an adequate time. GPUs (Graphics Processing Unit) and computer clusters are used for this.
RF-Frontend provides you with modern and powerful calculation methods and qualified expert knowledge for the modeling and simulation of your application.
Simulation of SMA to stripline transition
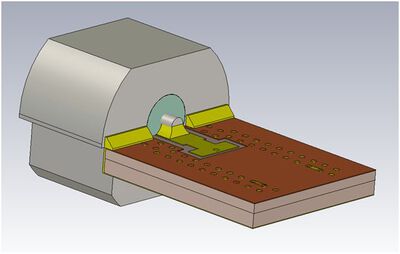
A very frequently occurring task is the optimization of RF connector transitions. The investigation can be performed relatively easily with a time domain simulator. The simulation results are evaluated by means of time domain reflectometry (TDR), since this method provides information about the location and type (inductive or capacitive) of the fault location. This enables a targeted optimisation.
The figure on the left shows the simulation model for the transition of an SMA connector to the 50 Ohm line in an inner layer.
Simulation results of SMA to stipline transition
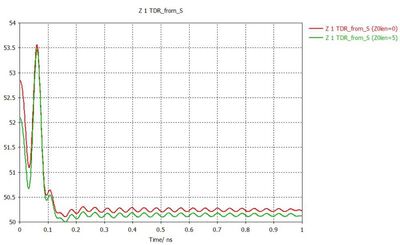
The adjacent figure shows the evaluation of the simulation results using TDR. In the front area of the plug, transition disturbances with inductive behaviour are recognizable which can be eliminated by specific measures.

